Event-Based Finite State Machines in Rust
While researching for other projects I've come across a number of different approaches to creating state machines in Rust.
This post is an example of my favorite pattern for an event-driven state machine implementation that produces clear and maintainable code.
The Pattern
The pattern consists of a few components:
- A
structthat acts as the machine itself, - A state
traitand several states - An
enumof events
The machine encapsulates the current state and any shared data.
The states are struct elements and all share a trait which ensures they have a compatible interface to handle events.
The events are inputs into the machine's states and can carry data. The states can respond to an event or ignore it.
A Trivial Example
The best way to share the pattern is probably with some code, so this is an trivial example that switches between two states.
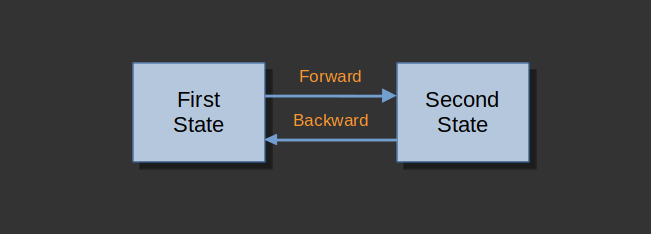
This machine has two states FirstState and SecondState, and two events Forward and Backward.
Note:
Later in this post we'll implement more useful machines. But by implementing this trivial machine first we can see the moving parts.
If you want to jump ahead:
The Machine
Building from the top-down, first we create a struct to act as the overarching machine.
struct StateMachine {
state: Option<Box<dyn State>>,
}
impl StateMachine {
fn handle_event(&mut self, event: Event) {
if let Some(state) = self.state.take() {
self.state = Some(state.handle_event(event, self));
}
}
}
It stores the current state as an Option<Box<dyn State>> trait object. And it implements a handle_event method which accepts an Event.
The machine's handle_event method calls the handle_event method on its current state, and then modifies the current state to be the result of that call. This allows us to implement transitions.
The State Trait
To have the trait object Box<dyn State> in the state machine, the states must all implement that shared State trait. This allows us to place any of them into the Box.
The trait looks like this:
trait State {
fn handle_event(self: Box<Self>, _event: Event, _state_machine: &mut StateMachine) -> Box<dyn State>;
}
This provides a common interface for the states, ensuring that they implement a handle_event method.
A state can return a different state (performing a transition) or it can return itself (no transition.)
The Actual States
Next we implement the actual states as structs that implement the trait.
struct FirstState {}
struct SecondState {}
impl State for FirstState {
fn handle_event(self: Box<Self>, event: Event, _state_machine: &mut StateMachine) -> Box<dyn State> {
match event {
Event::Forward => {
Box::new(SecondState {})
},
_ => {
self
}
}
}
}
impl State for SecondState {
fn handle_event(self: Box<Self>, event: Event, _state_machine: &mut StateMachine) -> Box<dyn State> {
match event {
Event::Backward => {
Box::new(FirstState {})
},
_ => {
self
}
}
}
}
The two states, FirstState and SecondState are structs which both implement the State trait. To satisfy the trait's contract, they both implement a handle_event method. Inside of that method they can either return a different state to transition or self to remain in the same state.
The first state matches the Forward event and returns a boxed up "SecondState". It ignores any other events by simply returning itself.
Likewise the second state matches the "Backward" event and returns the first state, while ignoring any other events.
The Events
Finally we implement the Event enum.
enum Event {
Forward,
Backward,
}
This enum enumerates the events we will want to use with the state machine, in this case Forward and Backward.
Using the Machine
As a reminder, the state diagram for our machine looks like this:

The code can be used like this:
fn main() {
// Create a new machine (defaulting in FirstState)
let mut machine = StateMachine { state: FirstState {} };
// Transition from FirstState to SecondState
machine.handle_event(Event::Forward);
// Transition from SecondState to FirstState
machine.handle_event(Event::Backward);
// An ignored event (the first state doesn't match this event)
machine.handle_event(Event::Backward);
}
While it did let us see the different parts in code, unfortunately this two-state machine is pretty useless as-is. There's no special logic, and the states don't do any useful work.
Let's implement something more substantial.
A Slightly More Complex Example
This is a slightly contrived demo for a state machine that holds a shared value. The states can do things with that value, such as read to it or write from it.
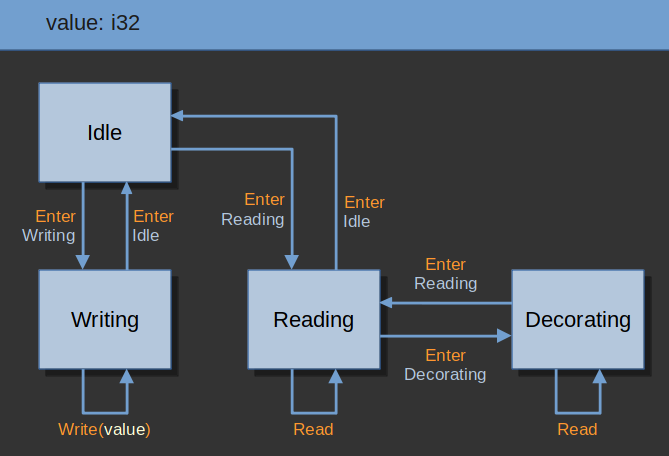
In this case the shared value is an i32 named value.
There is an initial Idle state that does no work but allows transitions to the Reading and Writing states.
As expected, the Writing state allows the value to be changed, and the Reading state allows the value to be read back.
There is also a Decorating state that can be reached from the Reading state which prints the value in a fancy way.
Creating the Machine
The struct for the machine looks similar to the trivial example, with the addition of the shared data.
struct StateMachine {
state: Option<Box<dyn State>>,
value: i32,
}
In this case the value: i32 is the shared data maintained by the struct.
impl StateMachine {
fn new() -> StateMachine {
StateMachine{
state: Some(Box::new(Idle {})),
value: 0,
}
}
fn handle_event(&mut self, event: Event) {
if let Some(state) = self.state.take() {
self.state = Some(state.handle_event(event, self));
}
}
}
The handle_event method is the same. And we now add a convenient New function to create machines in a consistent default state.
Adding States
The shared trait is identical to the earlier example.
trait State {
fn handle_event(self: Box<Self>, _event: Event, _state_machine: &mut StateMachine) -> Box<dyn State>;
}
We also need to add the Idle, Writing, Reading, and Decorating states.
The Idle state responds to two events (EnterReading and EnterWriting) to allow transitions to the Reading and Writing states.
It ignores all other events, simply returning itself.
struct Idle {}
impl State for Idle {
fn name(&self) -> &str {
"Idle"
}
fn handle_event(self: Box<Self>, event: Event, _state_machine: &mut StateMachine) -> Box<dyn State> {
match event {
Event::EnterReading => {
Box::new(Reading {})
},
Event::EnterWriting => {
Box::new(Writing {})
},
_ => {
self
}
}
}
}
The Reading state allows transitions to the Idle and Decorating states.
It also responds to the Read event to print the stored value from the machine. After reading it returns self to remain in the same state.
struct Reading {}
impl State for Reading {
fn name(&self) -> &str {
"Reading"
}
fn handle_event(self: Box<Self>, event: Event, state_machine: &mut StateMachine) -> Box<dyn State> {
match event {
Event::EnterIdle => {
Box::new(Idle {})
},
Event::EnterDecorating => {
Box::new(Decorating {})
},
Event::Read => {
println!("{}", state_machine.value);
self
},
_ => {
self
}
}
}
}
The Writing state can transition back to the Idle state.
It also responds to the Write(value) event to modify the value in the machine.
struct Writing {}
impl State for Writing {
fn name(&self) -> &str {
"Writing"
}
fn handle_event(self: Box<Self>, event: Event, state_machine: &mut StateMachine) -> Box<dyn State> {
match event {
Event::EnterIdle => {
Box::new(Idle {})
},
Event::Write(value) => {
state_machine.value = value;
self
},
_ => {
self
}
}
}
}
Finally, the Decorating state behaves like the Reading, also responding to the Read event. It just prints the value in a different way.
struct Decorating {}
impl State for Decorating {
fn name(&self) -> &str {
"Decorating"
}
fn handle_event(self: Box<Self>, event: Event, state_machine: &mut StateMachine) -> Box<dyn State> {
match event {
Event::EnterReading => {
Box::new(Reading {})
},
Event::Read => {
println!("_,-*`[ {} ]`*-,_", state_machine.value);
self
},
_ => {
self
}
}
}
}
Adding Events
Finally, we add the possible events to an enum like before.
enum Event {
EnterIdle,
EnterReading,
EnterWriting,
EnterDecorating,
Write(i32),
Read,
}
A notable difference this time is that the Write event contains an i32 value. This lets us send data along with the event.
An Example Program the Machine
As a reminder, the diagram for this machine looks like:

A program using this machine might look like:
fn main() {
let mut state_machine = StateMachine::new();
state_machine.handle_event(Event::Write(20));
state_machine.handle_event(Event::Read);
state_machine.handle_event(Event::EnterReading);
state_machine.handle_event(Event::Read);
}
This first creates the machine, which defaults in the Idle state.
We then send the Write and Read events with no effect because the Idle state ignores them.
Then we switch to the Reading state and send the Read event again. This time it prints the stored value (which is still 0 because the earlier write attempt was ignored.)
It prints:
0
fn main() {
// ...
state_machine.handle_event(Event::EnterDecorating);
state_machine.handle_event(Event::Read);
}
Then we can switch to the Decorating state and send the Read event again.
This prints:
_,-*`[ 0 ]`*-,_
fn main() {
// ...
state_machine.handle_event(Event::EnterReading);
state_machine.handle_event(Event::EnterIdle);
state_machine.handle_event(Event::EnterWriting);
state_machine.handle_event(Event::Write(5));
state_machine.handle_event(Event::EnterIdle);
state_machine.handle_event(Event::EnterReading);
state_machine.handle_event(Event::EnterDecorating);
state_machine.handle_event(Event::Read);
}
We then switch from the Decorating to the Reading state, then to the Idle state, and then to the Writing state (following the defined transitions), where we can send a Write event with a value of 5. We finally navigate all the way back to the Decorating state to read it.
This prints:
_,-*`[ 5 ]`*-,_
This implementation allowed us to switch between several states, and experience different behaviors in the program based on which state we were in.
Modeling a Mechanical Combination Lock
This final demo shows how states can decide to transition to different states depending on event or shared state conditions.
Here we implement a model of a combination lock that can switch between being opened, closed, or locked, depending on the provided events and inputs.
The state diagram for the machine looks like this:
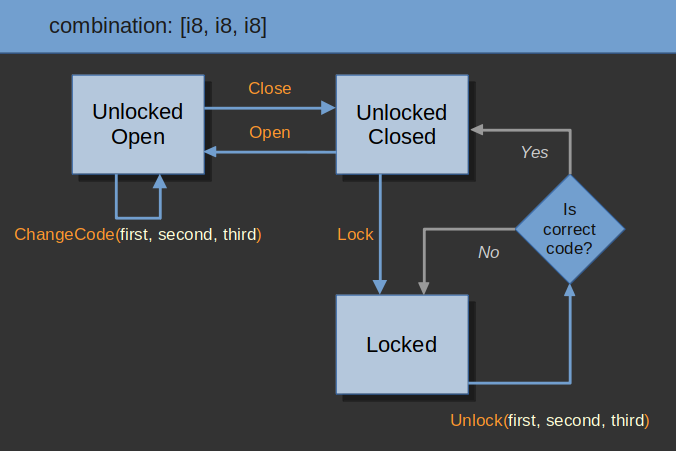
We can set a new combination when the lock is in the unlocked and open state.
We can open and close the lock by sending the events, but if we switch to the "Locked" state then we have to pass the condition to exit. The "Unlock" event needs to be sent with the correct combination to transition to the unlocked states again, otherwise it will stay locked.
Handling an Event with Conditions
We can build the state machine exactly like the previous examples.
The only change is that we modify the event handling in the Locked state like this:
struct Locked {}
impl State for Locked {
fn handle_event(self: Box<Self>, event: Event, lock: &mut Lock) -> Box<dyn State> {
match event {
Event::Unlock(first, second, third) => {
self.unlock(first, second, third, lock.combination)
},
_ => {
self
},
}
}
}
impl Locked {
fn unlock(self: Box<Self>, first: i8, second: i8, third: i8, combination: [i8; 3]) -> Box<dyn State> {
if [first, second, third] == combination{
Box::new(UnlockedClosed {})
} else {
self
}
}
}
It calls a method that compares the provided numbers with the combination in the machine. If they match then it switches to the UnlockedClosed state, if not it remains in the Locked state by returning self.
Mechanical Lock State Machine Code
An interactive command-line demo of the state of the mechanical lock machine mentioned above is available on my github: https://github.com/moonbench/rust-combo-lock-fsm:
It implements the state diagram from before:

With the addition of a command-line prompt that lets the user trigger events to affect the state machine:
Finite State Machine Lock Demo
________
| ____ |
| | | |
|_| | |
______|_| OPEN
| __ |
| [ ] |
| [] | UNLOCKED
| [] |
\______/
Enter command: set 11 12 13
[DONE] Code changed
________
| ____ |
| | | |
|_| | |
______|_| OPEN
| __ |
| [ ] |
| [] | UNLOCKED
| [] |
\______/
Enter command: close
[DONE] Lock closed
________
| ____ |
|_|____|_| CLOSED
| __ |
| [ ] |
| [] | UNLOCKED
| [] |
\______/
Enter command: lock
[DONE] Locked
________
| ____ |
|_|____|_| CLOSED
| __ |
| [**] |
| [] | LOCKED
| [] |
\______/
Enter command: open
[ERROR] Not allowed for a locked lock. Unlock it first.
________
| ____ |
|_|____|_| CLOSED
| __ |
| [**] |
| [] | LOCKED
| [] |
\______/
Enter command: unlock 0 0 0
[ERROR] Invalid combination, still locked
________
| ____ |
|_|____|_| CLOSED
| __ |
| [**] |
| [] | LOCKED
| [] |
\______/
Enter command: unlock 11 12 13
[DONE] Valid combination, unlocked!
________
| ____ |
|_|____|_| CLOSED
| __ |
| [ ] |
| [] | UNLOCKED
| [] |
\______/
Enter command: open
[DONE] Lock opened
________
| ____ |
| | | |
|_| | |
______|_| OPEN
| __ |
| [ ] |
| [] | UNLOCKED
| [] |
\______/
